Наука и образование: парадокс дней рождения и другие парадоксы

Наука и образование: парадокс дней рождения и другие парадоксы
Художник: Роман Перец
Всё, что не имеет логического объяснения, делает нас сильнее. Парадоксы — плод нашего ума, отбившийся от рук.
Мы охотнее жертвуем своей жизнью, чем деньгами; актёр, исполняющий роль доктора, зарабатывает больше, чем среднестатистический врач; история нас учит только тому, что история нас ничему не учит; чем больше самоубийц, тем меньше самоубийц; а когда мы выбираем меньшее из двух зол, нас непременно настигает большее.
Мы ведём себя парадоксально и непредсказуемо, и так было всегда. А что самое замечательное — наша же противоречивость порой помогает нам разрешить некоторые проблемы и объяснить некоторые поступки. Давайте рассмотрим несколько самых известных парадоксов: и логических, и математических, и общечеловеческих: парадокс дней рождения, дилемма заключённого и другие.
ЛОГИЧЕСКИЕ ПАРАДОКСЫ
ПАРАДОКС КРОКОДИЛА
Крокодил крадёт ребёнка у матери и обещает ей отдать его только в случае, если она правильно ответит на вопрос: отдаст ли он ей ребёнка? Если она ответит неправильно, то ребёнка мать не получит.
Мать: Не отдашь.
Крокодил: Ну ок, ты либо ответила верно, либо неверно. Если ты ответила верно, что я тебе не отдам ребёнка, я не отдам тебе его, потому что иначе твои слова будут неверны. Если ты ответила неверно, то тогда я тебе не могу отдать ребёнка по нашему договору.
Мать: Нет, но если я ответила верно, ты должен мне отдать ребёнка, как мы и договорились. А если моё утверждение о том, что ты мне его не отдашь, неверно, — ты всё равно должен мне его отдать, ведь это будет значить, что верно утверждение о том, что ты мне его отдашь.
Этот парадокс — классический случай самореференции (когда понятие ссылается само на себя). Такой же принцип лежит внутри парадокса лжеца: «То, что я утверждаю сейчас — ложно»; или парадокса всемогущества: «Может ли всемогущий создать камень, который не сможет поднять?»
ПАРАДОКС КУЧИ
В какой момент куча перестаёт быть кучей, если от неё постепенно отнимать по одной песчинке?
Одно зёрнышко — это не куча. Добавление одного зёрнышка не может считаться существенным для образования кучи. Исходя из этого парадокса, сколь угодно большое количество зёрен не сможет образовать кучу, но тогда ставится под сомнение сам факт существования кучи.
Парадокс кучи основан на нечётких множествах, с которыми тоже можно проводить достаточно чёткие математические операции. Например, в разделе информатики, которая изучает нейронные сети и искусственный интеллект, помимо традиционных значений Истина и Ложь вводятся дополнительные: Возможно, Иногда, Почему бы и нет, Ещё не решил и т. д. Это нужно как раз для того, чтобы компьютер мог смоделировать поведение человека, которому не свойственно видеть мир в чёрно-белых тонах.
Если мыслить не категориями множеств, а целыми бесконечностями, можно дойти до знаменитой дихотомии — стрелы Зенона:
Летящая стрела неподвижна, так как в каждый момент времени она занимает равное себе положение, то есть покоится; поскольку она покоится в каждый момент времени, то она покоится во все моменты времени, то есть не существует момента времени, в котором стрела совершает движение.
Апории Зенона до сих пор не разрешены, но вся суть споров сводится к тому, что математические рассуждения, применимые к бесконечности, неприменимы к реальному миру, в котором нет «точки пространства» и «момента времени». А есть только миг между прошлым и будущим.
МАТЕМАТИЧЕСКИЕ ПАРАДОКСЫ
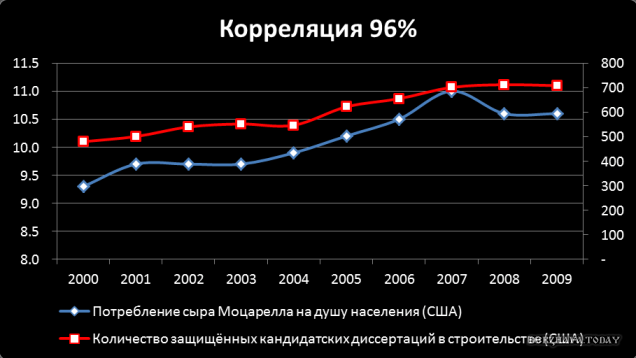
ЛОЖНАЯ КОРРЕЛЯЦИЯ
Ложная корреляция — коварная вещь. Когда две независимые друг от друга величины меняются синхронно, велик соблазн выстроить между ними причинно-следственную связь. Эта связь кажется очевидной и даже выглядит вполне достоверно, но она фальшива.
Примеров множество:
Чем больше церквей в городе, тем сложнее в нём криминогенная обстановка.
Конечно, ведь большое количество церквей обычно возникает в крупных городах, которым свойствен повышенный уровень преступности.
Чем больше пожарных тушат пожар, тем сильнее вызванные пожаром разрушения. Значит ли это, что разрушения вызываются именно пожарными?
Такую зависимость можно вывести из каких угодно случайных фактов, если проследить кривую их роста и увидеть, что они поразительно похожи. Существует даже целый сервис, посвящённый любопытным корреляциям, используемым для доказательства любой, даже самой странной теории.
ФЕНОМЕН УИЛЛА РОДЖЕРСА
Когда жители Оклахомы переезжают в Калифорнию, они повышают среднее значение IQ обоих штатов.
Эту цитату приписывают американскому комику Уиллу Роджерсу, отсюда и название.
Предположение, что перемещение объектов из одного множества в другое может увеличить среднее значение обоих множеств, лишь кажется парадоксальным. На самом деле такое вполне может происходить.
Возьмём, к примеру, сотрудников отдела продаж ООО «Бесперспективность». У компании есть несколько филиалов со своими отделами продаж. Филиал в Сокольниках демонстрирует стабильно лучшие показатели, чем филиал в Южном Бутово. Чтобы спасти своих менеджеров по продажам, хитрый директор Южно-Бутовского офиса предлагает дирекции провести манёвр: перевести двух худших сотрудников лучшего отдела из Сокольников в свой филиал. Производительность обоих отделов в среднем от такого перемещения только увеличится: станут выше средние показатели лучшего отдела без сравнительно вялых для него сотрудников; и они же окажутся бравыми орлами для Южного Бутово.
На цифрах это тоже работает:
A = {1, 2, 3, 4},
B = {5, 6, 7, 8, 9}.
Среднее арифметическое множества А — 2,5; множества В — 7.
Если из множества B перевести число 5 во множество А:
A = {1, 2, 3, 4, 5},
B = {6, 7, 8, 9}.
Среднее арифметическое множества А — 3; множества В — 7,5.
ВЕРОЯТНОСТНЫЕ ПАРАДОКСЫ
ПАРАДОКС ДНЕЙ РОЖДЕНИЯ
Наверняка, когда вы учились в школе, хотя бы у пары ваших одноклассников дни рождения приходились на один день. Почему так происходит, ведь дни рождения могут выпадать на 365 (366 в случае високосного года) разных дат, а в классе было не более 30 человек? Совпадение это или закономерность?
Это и есть парадокс дней рождений.
Если у вас в классе или в коллективе хотя бы 23 человека, вероятность того, что у кого-то из них дни рождения совпадут, превышает 50%.
Собственно, это и парадоксом назвать сложно, поскольку математический расчёт вероятности это неоспоримо доказывает. Но большинству людей трудно поверить в то, что группы из 23 людей достаточно для того, чтобы дни рождения у её участников совпали в половине случаев.
Мы не будем здесь приводить математическую формулу вероятностного расчёта (её можно посмотреть в Википедии), но если посмотреть на задачу несколько под другим углом, становится проще смириться с этим фактом. Например, если взять 1 000 групп по 23 человека, то как минимум в 500 из них окажутся люди с совпадающими днями рождения. А это звучит уже не так удивительно.
Парадокс дней рождений работает при оценке популяции рыб в озёрах, когда рыбу ловят, помечают и отпускают. Вероятность поймать уже помеченную рыбу будет расти нелинейно; а значит, уже после первой пойманной помеченной рыбы можно грубо оценить популяцию.
ПАРАДОКС МОНТИ ХОЛЛА
Эта вероятностная задачка названа в честь ведущего американского шоу Let’s Make a Deal. Звучит он так:
Вы — участник игры, в которой можно выиграть автомобиль. Перед вами три двери. За одной из них находится автомобиль, за двумя другими — козы. Вы выбираете одну из дверей. Ведущий знает, где находится автомобиль, и открывает одну из дверей, за которой находится коза. После этого он просит вас выбрать ещё раз.
Вопрос: увеличатся ли ваши шансы выиграть автомобиль, если вы измените свой выбор?
Стандартный ответ: нет, ведь в любом случае останутся две двери, за одной из которых есть автомобиль. Так что шансы 50/50 вне зависимости от первоначального выбора.
Правильный ответ: если игрок изменит выбор, он выигрывает с вероятностью 2/3. Снова опускаем формулы и рассуждаем бытовым языком. Предположим, что у вас есть множество попыток сыграть в эту игру, и вы каждый раз изменяете свой выбор. В каком случае вы проиграете? Только если вы изначально выбрали «дверь с автомобилем». Если вы изначально сделали неверный выбор, вы выиграете. А вероятность выбрать «дверь с козой» на первом этапе составляет 2/3 (ведь двери три, а козы две). Получается, что на первом этапе у вас больше шансов ошибиться, а значит, изменив выбор на втором этапе, у вас больше шансов выиграть.
ПАРАДОКСЫ ПРИНЯТИЯ РЕШЕНИЙ
ДИЛЕММА ЗАКЛЮЧЁННОГО
Классическая и всегда актуальная задача в теории игр и основной элемент практически всех криминальных драм.
Сама ситуация такова:
Полиция поймала двоих подозреваемых в преступном сговоре. Полицейские изолировали их друг от друга и поставили обоих перед одним и тем же условием: если один свидетельствует против другого, а тот хранит молчание, то первый освобождается за помощь следствию, а второй получает максимальный срок лишения свободы (10 лет). Если оба молчат, их деяние проходит по более лёгкой статье, и каждый из них приговаривается к 0,5 года. Если оба свидетельствуют против друг друга, они получают минимальный срок (по 2 года). Каждый заключённый выбирает, молчать или свидетельствовать против другого. Однако ни один из них не знает точно, что сделает другой. Что произойдёт?
Логично предположить, что самая выгодная стратегия с минимальными рисками для обоих — молчать, а не предавать. Суть дилеммы: игроки не всегда будут сотрудничать друг с другом, даже если в итоге приведёт к максимальной выгоде для обеих сторон, предпочитая краткосрочную выгоду только для себя.
Производная от этой дилеммы — «обмен закрытыми сумками» — выворачивает дилемму заключённого наизнанку.
Два человека встречаются и обмениваются закрытыми сумками, понимая, что одна из них содержит деньги, другая — товар. Каждый игрок может уважать сделку и положить в сумку то, о чём договорились, либо обмануть партнёра, дав пустую сумку.
Здесь же очевидно, что лучшим решением является обман. Именно поэтому игра с закрытыми сумками — то, что принято избегать в цивилизованном обществе. Хотя гонка вооружений работает именно по принципу закрытых сумок.
А закончим мы парадоксом, который поставит полезность этой статьи под сомнение:
ПАРАДОКС ИНТЕРНЕТА
Вероятность существования нужной информации в Интернете возрастает, а возможность её найти уменьшается.
Поднимем вероятность нахождения ненужной информации и предложим ещё несколько ссылок из рубрики «Наука и образование»: «Наука и образование: Человек против компьютера», «Ноам Хомский», «Память и мнемотехника», «Классический миф», «Удивительная химия», «Прекрасные галактики». А чтобы прочитать о когнитивных искажениях, зайдите в этот блог.
Просмотры: 357




